Elementary particles theory
Let’s express equation system of physical vacuum dynamics through spherical coordinates and consider only specific
solutions of resulting equation system, in which component 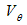 of perturbation propagation velocity
of perturbation propagation velocity 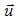 by radius r and angles
by radius r and angles 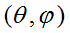 equals zero.
Other components will be designated as
equals zero.
Other components will be designated as
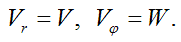
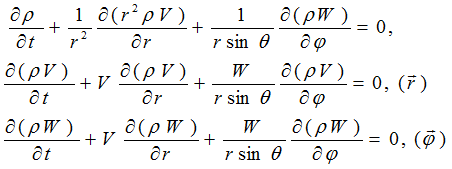
 which define vector directions of corresponding equation lines, are in brackets after equations. Let’s show
that obtained equation system has solutions, which possess all known properties of elementary particles when r
is small. These solutions will be sought as waves propagating with constant angular velocity by the angle
which define vector directions of corresponding equation lines, are in brackets after equations. Let’s show
that obtained equation system has solutions, which possess all known properties of elementary particles when r
is small. These solutions will be sought as waves propagating with constant angular velocity by the angle
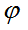 under the influence of small-amplitude oscillations of physical vacuum density:
under the influence of small-amplitude oscillations of physical vacuum density:
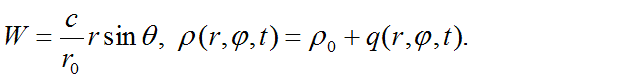
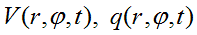 are both small when r. is small.
Under such problem formulation, each elementary particle is sphere of radius r0,
inside of which waves, created by small-amplitude oscillations of
physical vacuum density, propagating along to any parallel (circle with
radius
are both small when r. is small.
Under such problem formulation, each elementary particle is sphere of radius r0,
inside of which waves, created by small-amplitude oscillations of
physical vacuum density, propagating along to any parallel (circle with
radius
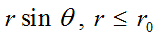 ) with constant angular velocity (frequency) c/r0,
making full roundabout way by angle
) with constant angular velocity (frequency) c/r0,
making full roundabout way by angle 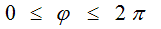 over equal time
over equal time 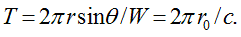 In addition, linear velocity of these waves increases linearly with the radius, reaching its maximum value (speed of light с) on sphere’s equator when
In addition, linear velocity of these waves increases linearly with the radius, reaching its maximum value (speed of light с) on sphere’s equator when
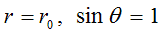 (Fig.1)
(Fig.1)
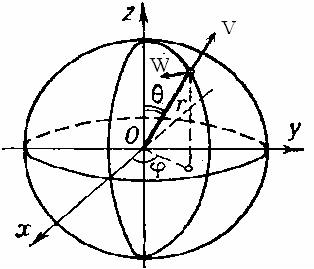
Fig.1. Schematic representation of elementary particle.
Substitution of assumed form of solutions into physical equations system of elementary particles with a drop of second infinitesimal order terms and multiplications of small terms, one can obtain its solutions in the following form
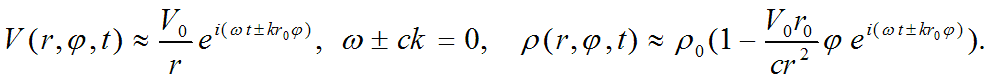
It’s worth a notion that at such approximation nonlinear term of second infinitesimal order
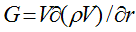 .
has been entirely neglected. This term exactly generate gravitational field of a particle, but its role becomes significant only with relatively large r.
.
has been entirely neglected. This term exactly generate gravitational field of a particle, but its role becomes significant only with relatively large r.
However, not every obtained wave solution is an elementary particle. Such solution has to have electric field and spin, possess properties of charge conservation and universality, as well as quantum properties of mass, momentum and energy. Moreover, over the time of full roundabout way of the wave along the sphere equator, electric field intensity must conserve its sign. All these classical and quantum mechanical terms need correct definitions through the characteristics of physical vacuum.
First, let’s give the definition of electric field intensity and electric charge of elementary particle similarly to the case of plane electromagnetic waves propagation in electrodynamics of physical vacuum.
Definition. Electric field intensity 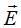 and charge density distribution
ρch of elementary particle will be defined as:
and charge density distribution
ρch of elementary particle will be defined as:
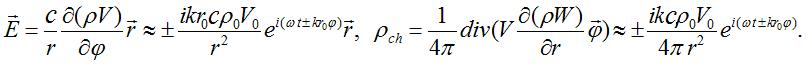
It’s worth a notion that like in the case of plane electromagnetic
waves, electric field intensity vector is only a linearization of a real
field vector
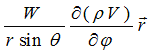 and coincides with it only on equator of the sphere with radius r0.
and coincides with it only on equator of the sphere with radius r0.
Let’s determine the charge qch of elementary particle, integrating the stationary density distribution of charge over sphere’s volume with radius r0:
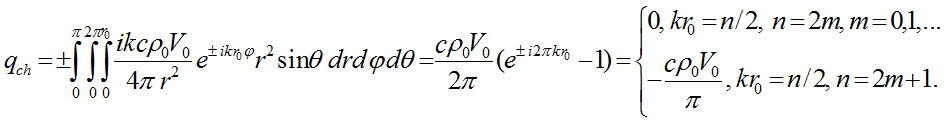
It follows from the last formula that only cases, when wave number kr0 is an integer or a half-integer value, correspond to elementary particles. For integer value of kr0 the charge is zero, for any half-integer value of kr0 charge equals common by modulus value
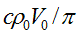 , which is negative when wave is propagating in direction of angle
, which is negative when wave is propagating in direction of angle 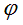 increment (с has a positive sign), and positive when wave is
propagating in opposite direction (с has a negative sign). Furthermore
time,
increment (с has a positive sign), and positive when wave is
propagating in opposite direction (с has a negative sign). Furthermore
time,
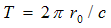 of the wave’s full roundabout way by angle
of the wave’s full roundabout way by angle
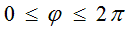 along any parallel of the sphere with radius r0 equals integer number 2kr0
of half-periods
along any parallel of the sphere with radius r0 equals integer number 2kr0
of half-periods 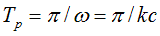 physical vacuum oscillations and electric field intensity, which
conserves its sign on the last uneven half-period, being equal to the
charge’s sign.
physical vacuum oscillations and electric field intensity, which
conserves its sign on the last uneven half-period, being equal to the
charge’s sign.
Notice that resulting solution can be interpreted as photon spiral wave bifurcation with wavelength λ=2π/k curled around the circle with radius r0=1/k, in such way, that its wavelength equals the circle’s perimeter (see electrodynamics of physical vacuum). At collision with an obstacle and compression of a photon there are solutions of physical equations system of elementary particles as two waves of compression - stretchings of density of physical vacuum, propagating along an angle φ in opposite directions with ρ=ρ0+q0ei(ωt±kr0φ) and V=0. Therefore the creation of any elementary particle can be treated as its bifurcation from curled photon with appropriate wavelength. In that case the wavelengths of created periodic solutions (particle and antiparticle) are less than corresponding photon’s wavelength in half-integer value of times.
It can be shown that electric field intensity and charge of elementary particle defined above agree with electromagnetic form of Dirac equation for electron in neighborhood of equator of the sphere with radius r0:
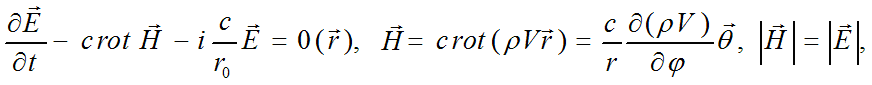
where magnetic field intensity vector is a virtual one, since it’s aligned by angle
 ,
while velocity vector component
,
while velocity vector component  over this angle equals zero. Therefore, there is no real magnetic field of an elementary particle.
From the second equation of equations system of elementary particles one can obtain with
ignorance of the second (gravitational) term the second order wave equations of vector
over this angle equals zero. Therefore, there is no real magnetic field of an elementary particle.
From the second equation of equations system of elementary particles one can obtain with
ignorance of the second (gravitational) term the second order wave equations of vector
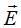 :
:
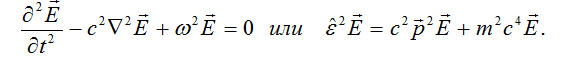
where
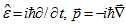 are operators of energy and momentum, and
are operators of energy and momentum, and 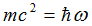 .
Therefore, the true physical meaning of wave function ψ
from Dirac equation for electron in bispinor form becomes clear – it’s a vector of particle’s electromagnetic wave, magnetic
field in such case is exclusively virtual. It’s important to point out that outer electric field of elementary particle
directed along radius is created by particle’s electric charge, but at the same time the charge is divergence of a
completely different inner field of the particle, which is represented by second and third terms in the third equation
of equations system of elementary particles and directed by angle
.
Therefore, the true physical meaning of wave function ψ
from Dirac equation for electron in bispinor form becomes clear – it’s a vector of particle’s electromagnetic wave, magnetic
field in such case is exclusively virtual. It’s important to point out that outer electric field of elementary particle
directed along radius is created by particle’s electric charge, but at the same time the charge is divergence of a
completely different inner field of the particle, which is represented by second and third terms in the third equation
of equations system of elementary particles and directed by angle 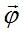 .
Also notice that outer electric field intensity of elementary particle
decreases with the distance from center of the particle as
1/r2, and that agrees with Coulomb’s law, but inside the particle (that is within the sphere of radius r0 )
the intensity of a real (not linearized) electric field decreases as 1/r(!), so it removes the problem of infinite energy and mass of elementary particles.
.
Also notice that outer electric field intensity of elementary particle
decreases with the distance from center of the particle as
1/r2, and that agrees with Coulomb’s law, but inside the particle (that is within the sphere of radius r0 )
the intensity of a real (not linearized) electric field decreases as 1/r(!), so it removes the problem of infinite energy and mass of elementary particles.
Let’s now determine internal energy ε of an elementary particle with a use of expression for a work executed by the sum of all
internal field forces of the particle, directed on a vector 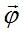 ,
over all charges determined by divergence of this common field:
,
over all charges determined by divergence of this common field:
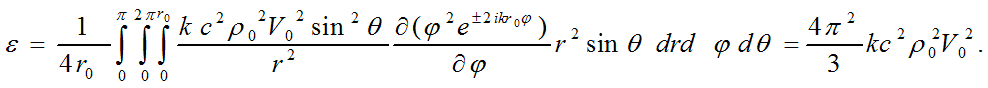
Now, to derive the well-known formulas and correlations of quantum mechanics, it’s suffice to denote the mass of elementary particle as
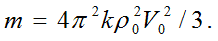 After this one can immediately obtain: Einstein’s formula for internal energy of a particle ε=mc2,
Planck's resulted constant
After this one can immediately obtain: Einstein’s formula for internal energy of a particle ε=mc2,
Planck's resulted constant 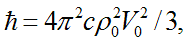 formulas of impulse and energy for de Broglie’s waves
formulas of impulse and energy for de Broglie’s waves
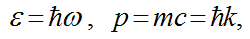 formula for the spin of an elementary particle
formula for the spin of an elementary particle 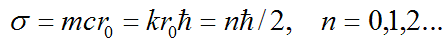 ,
fine structure constant formula
,
fine structure constant formula 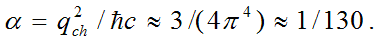
These formulas, derived exclusively by the methods of classical mechanics, are completely identical to the well-known expressions of quantum mechanics as well as clearly reflect the physical essence of charge, mass, energy and spin of elementary particles, allowing to understand the nature of quantum processes in microcosm. It can be seen that the internal energy of the particle is indeed proportional to the square of velocity of light, and proportionality coefficient (mass of the particle) linearly grows with the increase of wave number k, as well as frequency ω of the parental photon. The Plank’s resulted constant is indeed a constant value depending only on characteristics of physical vacuum and not on the type of the elementary particle. The spin of the particle indeed has a value of either integer or half-integer number of ħ, which allows to separate all elementary particles in two general categories: bosons and fermions. Still, the most surprising and encouraging fact is the almost precise match of the fine structure constant α with its experimental value 1/137.
Let’s notice, that more complex, multi-curled elementary particles correspond to high-frequency perturbation waves with bigger mass and energy. It’s natural to imply that the simplest half-curled particles with the spin of 1/2 when n = 1 are pairs “electron-positron”. That way, electron is a double period cycle in relation to the initial cycle defined by the motion of curled photon. That brings another proof of the theory introduced in this research – the interpretation of the Pauli principle, the corollary fact of which is that electron returns to the initial state only after the turn of 720, not 360 degrees. According to R. P. Feynman, particle with topology of Moebius band meets the Pauli principle. But in the Feigenbaum-Sharkovskii-Magnitskii universal theory of dynamical chaos (FSM theory), results of which valid for every nonlinear differential equations system of macrocosm, the solution’s difficulty increase starts from double period bifurcation of the initial singular cycle. Interesting enough, the newborn cycle of doubled period belongs to the Moebius band around the initial cycle! In another words, according to the FSM theory electron is an initial and simplest double period bifurcation from the infinite bifurcation cascade. Therefore, FSM theory works not only in macro-, but also in microcosm, and elementary particles defined here are hardly the only elementary particles, which can emerge as the result of bifurcations in nonlinear equations system of dynamics of physical vacuum. Furthermore, more complex nonperiodic solutions of this system can be foreseen, which are singular attractors in terms of FSM theory. Thus, any attempts of an experimental detection of the simplest (most elementary), as well as the most complex of particles are essentially futile.
Let's note also, that as the length of an electron wave twice is more than the length of a wave of a parental photon, and frequency of fluctuations twice is less, i.e ωph=2ωe that from the equation of the curled photon follows, that in a vicinity of equator of sphere of radius r0 Schrodinger's equation for a free particle takes place
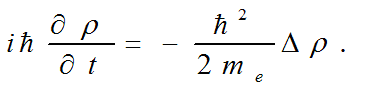
That is the wave of compression - stretching of density of physical vacuum propagating along an angle φ satisfies the Schrodinger's equation in a vicinity of equator of a sphere of an elementary particle . Thus there is clear a physical sense of ψ - function in Schrodinger's equation - it is a density of physical vacuum. It can be shown also that the scalar function E* which is complex connected to the module of electric field intensity also satisfies Schrodinger's equation.
- Nikola Tesla
- Feigenbaum-Sharkovskii-Magnitskii (FSM) theory
- Theory EDCW (electrodynamics of curvilinear waves) of A.Kyriakos
- Electrodynamics of physical vacuum
- Theory of elementary particles
- Gravitation and gravitational waves
- Author: Magnitskii N.A.



