Electrodynamics of physical vacuum
Let’s consider a case in which perturbation propagation velocity 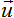 has a certain direction in physical vacuum set by unit vector
has a certain direction in physical vacuum set by unit vector 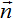 .
Solutions of the system of equations of physical vacuum would be searched in the form of:
.
Solutions of the system of equations of physical vacuum would be searched in the form of:
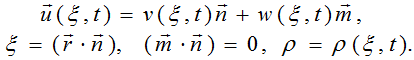
One can obtain a system of the equations for functions ρ(ξ,t),v(ξ,t),w(ξ,t)
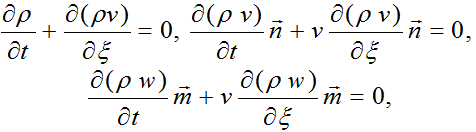
which would be called the the system of the equations of electrodynamics of physical vacuum.
In the particular case of transverse fluctuations of physical vacuum of constant density
(ρ(ξ,t)=ρ0=const)
and distribution of these fluctuations in a longitudinal direction with constant velocity v(ξ,t)=c
the system of equations of electrodynamics of physical vacuum can be reduced to one equation in one complex variable w(ξ,t)
Let's introduce into consideration vectors of electric 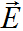 and magnetic
and magnetic 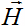 fields intensities by the formulas:
fields intensities by the formulas:
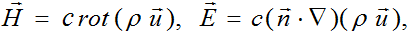
By consistently applying the operators сrot and c(
 •∇) to the function
w(ξ,t)
we shall obtain the classical system of Maxwell's equations describing
the propagation of electromagnetic waves in the so-called empty space
(vacuum):
•∇) to the function
w(ξ,t)
we shall obtain the classical system of Maxwell's equations describing
the propagation of electromagnetic waves in the so-called empty space
(vacuum):
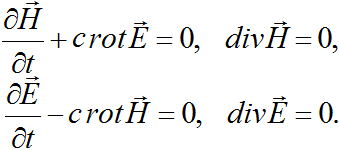
The system of Maxwell's equations has a solution in the form of
 =
=
 0
ei(ωt - kξ),
Let’s consider that the real parts of their complex expressions have
physical sense. They determine an in-phase plane transverse
electromagnetic wave, propagating with a speed of light c in any direction set by an unit vector
0
ei(ωt - kξ),
Let’s consider that the real parts of their complex expressions have
physical sense. They determine an in-phase plane transverse
electromagnetic wave, propagating with a speed of light c in any direction set by an unit vector
 . The unique characteristic of a classical plane electromagnetic wave is its frequency
ω (or its wavelength λ=2πc/ω).
Note, that in-phase vectors of electric and magnetic fields intensities periodically vanish simultaneously.
This fact contradicts the law of conservation of energy and raises doubts about validity of classical interpretation
of an electromagnetic wave in which a change of the electric field causes a change in the magnetic field and vice versa.
. The unique characteristic of a classical plane electromagnetic wave is its frequency
ω (or its wavelength λ=2πc/ω).
Note, that in-phase vectors of electric and magnetic fields intensities periodically vanish simultaneously.
This fact contradicts the law of conservation of energy and raises doubts about validity of classical interpretation
of an electromagnetic wave in which a change of the electric field causes a change in the magnetic field and vice versa.
In turn, the system of equations of electrodynamics of physical
vacuum has a solution in form of spiral wave of constant amplitude w(ξ,t)
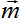 = (w * +
w0 ei(ωt - kξ))
= (w * +
w0 ei(ωt - kξ))
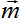 , ω = kс,
propagating with velocity c in physical vacuum in a direction of a vector
, ω = kс,
propagating with velocity c in physical vacuum in a direction of a vector 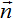 with conservation of energy carried by the wave and having arbitrary constant shift w*
in a direction of a vector
with conservation of energy carried by the wave and having arbitrary constant shift w*
in a direction of a vector 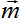 . In such formulation the speed of light c
in empty space has a clear physical sense - it is the propagation
velocity of perturbations of physical vacuum of constant density
in the absence of matter (see elementary particles).
And since in this case the vectors
. In such formulation the speed of light c
in empty space has a clear physical sense - it is the propagation
velocity of perturbations of physical vacuum of constant density
in the absence of matter (see elementary particles).
And since in this case the vectors 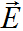 and
and
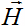 of a classical plane electromagnetic wave are a directional derivative and a rotor of a vector
ρ0w(ξ,t)
of a classical plane electromagnetic wave are a directional derivative and a rotor of a vector
ρ0w(ξ,t) 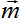 ,
it is possible to conclude, that the classical electromagnetic wave is an artificial form and is completely
determined by the spiral wave of perturbations propagation in physical vacuum (Fig.1).
,
it is possible to conclude, that the classical electromagnetic wave is an artificial form and is completely
determined by the spiral wave of perturbations propagation in physical vacuum (Fig.1).
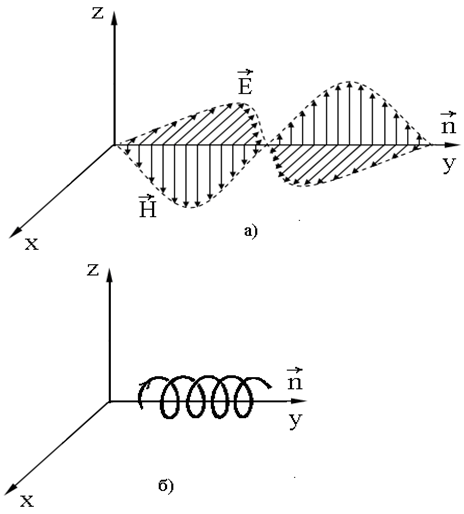
Fig.1. Propagation of a classical plane electromagnetic wave (a) and a spiral wave of physical vacuum (b).
Now we can compare the spiral wave in the physical vacuum, obtained as the solution of the system of equations which are invariant under Galilean transformations, and the classical electromagnetic wave, obtained as the solution of system of Maxwell's equations. Both waves have an arbitrary frequencies and corresponding wavelengths, so the two solutions describe all plane transverse electromagnetic waves existing in nature. However, as it could be easily seen from the analysis above, the vectors of classical electric and magnetic fields are artificial vectors, namely, the derivatives of the same true vector of the velocity perturbations propagation in the physical vacuum. Hence, there are no solutions corresponding to the constant shiftw* of transverse wave of physical vacuum in the form of classical electromagnetic waves that can be derived from Maxwell’s equations. This is the main reason that Maxwell's equations are not invariant under Galilean transformations, and, moreover, they cannot be modified so that they would satisfy these transformations
Furthermore, a classical electromagnetic wave (Fig. 1а) does not allow to correctly define the concept of a quantum of electromagnetic waves (photon), because apart from wavelength λ needs it also requires the value of the oscillation amplitude. The kind of a spiral wave of perturbations propagation in physical vacuum allows the unique determination of the photon - it's a part of the cylindrical volume of the physical vacuum under a spiral of a wavelength λ and radius r0=c/ω. Wave motion on a spiral inside the given volume occurs with a constant angular velocity ω, and linear velocity reaches its maximum value (the speed of light c) on the lateral surface of the cylinder. Elementary particles and antiparticles in the form of balls of radius r0(see elementary particles).
Let’s consider now the general case of propagation of spiral waves
in physical vacuum of variable density. Through the application of
operators
сrot, c
(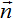 •∇) to the sum of the second and the third equations of system of equations of
electrodynamics of physical vacuum and taking into account the linear charge density
ρch and current density
•∇) to the sum of the second and the third equations of system of equations of
electrodynamics of physical vacuum and taking into account the linear charge density
ρch and current density 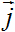 out of formulas
out of formulas
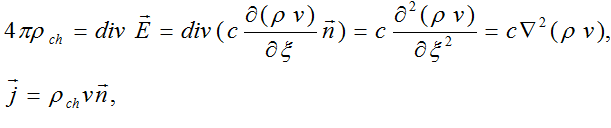
we shall obtain the system of equations for electric and magnetic fields intensities
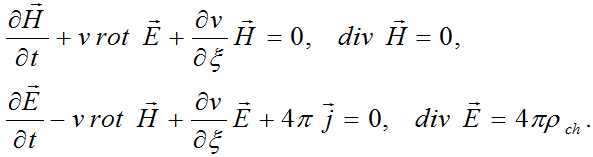
Note that in this case the electric field intensity vector 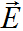 has a nonzero longitudinal component even at v=c=const,
when the last system of equations is a classical system of Maxwell's equations in the presence of charges and currents.
It follows from here that a current in the sense of classical system of Maxwell's equations is not the motion of charges,
but it is the second derivative (Laplacian) from longitudinal wave of periodic physical vacuum density’s compression -
stretching propagating with the speed of light. It also follows that charges and currents can exist in physical vacuum
even at the absence of substance (matter) in it.
has a nonzero longitudinal component even at v=c=const,
when the last system of equations is a classical system of Maxwell's equations in the presence of charges and currents.
It follows from here that a current in the sense of classical system of Maxwell's equations is not the motion of charges,
but it is the second derivative (Laplacian) from longitudinal wave of periodic physical vacuum density’s compression -
stretching propagating with the speed of light. It also follows that charges and currents can exist in physical vacuum
even at the absence of substance (matter) in it.
, from validity of a postulate on existence of physical vacuum (ether) follows, that: 1) Maxwell's equations describe distribution of plane electromagnetic waves in moving inertial References frames only approximately for small speeds of movement of such systems relatively to the speed of light; 2) there exist more general equations deduced from the equations of physical vacuum and laws of classical mechanics which are invariant concerning Galilean transformations and precisely describe distribution of plane electromagnetic waves in any moving inertial References frame; 3) conclusions of modern physics about absolutization of system of Maxwell's equations, about incorrectness of the equations of classical mechanics, and also the basic postulate of the special theory of relativity on a constancy of speed of light in any inertial References frame are erroneous.
- Nikola Tesla
- Feigenbaum-Sharkovskii-Magnitskii (FSM) theory
- Theory EDCW (electrodynamics of curvilinear waves) of A.Kyriakos
- Electrodynamics of physical vacuum
- Theory of elementary particles
- Gravitation and gravitational waves
- Author: Magnitskii N.A.



